房贷与货币的时间价值（Mortgage and the time value of money）

知乎上看到一个问题“30年的房贷利息几乎等于本金，你是怎么看的？”。虽然我们都知道因为通膨，问题并不能如此简单粗暴地看待，不过这里最高赞的回答还是深入浅出，所以在此系统地整理了一下。

首先，要指出的一点是：仅仅观察房贷的利息是没有意义的。这是因为各年的利息不能简单的加起来，而要折现。换句话说，价格不是一个固定的参考系。一个简单例子就是大家多少都听说过的通膨。

关于通膨，有一个国际通用的所谓的“The Big Mac index”，这里“Big Mac”即麦当劳经典巨无霸汉堡。参考下图，我们发现巨无霸在2000年的时候是9.9元（图中为美元，此处已经折算成人民币），2008年的时候是12.5元，2015年的时候是17.2元，而2020的时候是21.5元。这里需要注意的一点是，不同的物品，通货膨胀是不一样的。

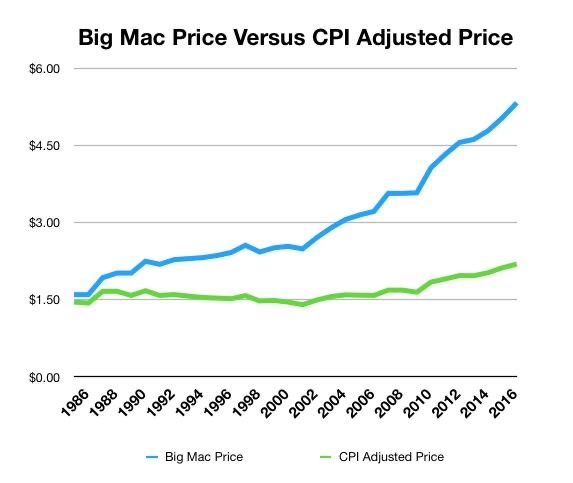
正是因为每年的物价都不一样，所以当我们比较不同年份的金钱的时候需要打一个折扣，即所谓的货币的时间价值（the Time Value of Money， TVM）。最简单的做法就是选一个基准年份$t_0$，随后每个年份$t_1\geq t_0$的价格都除以$(1+r)^{(t_1-t_0)}$。这里$r$就是所谓的折现率，我们简单假设它是一个很小的正实数且是一个常数（不随年份变化）。

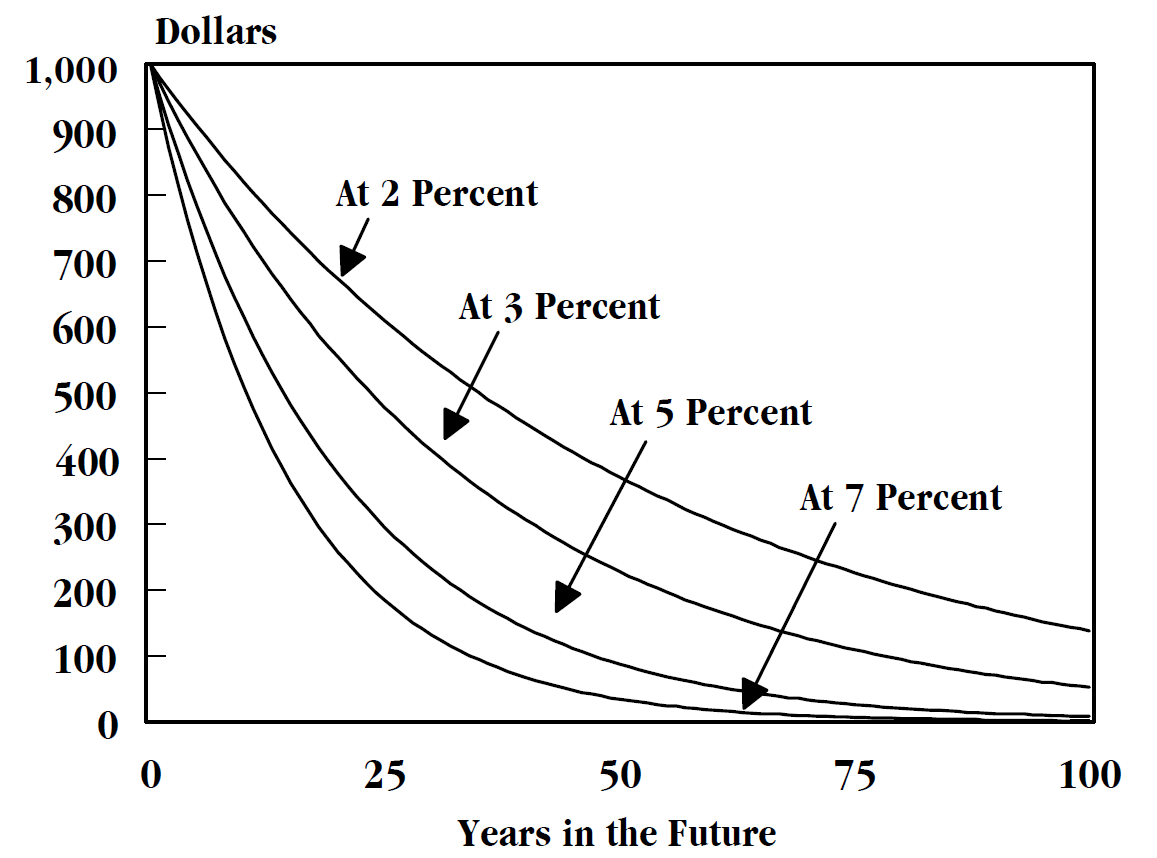
上图来自维基百科，就画出了未来某个年份（横轴）1000元对应现在的价值。假设折现率$r=0.03$，那么25年后的1000元相当于现在的$1000/(1+0.03)^{25}\approx 447.61$元，50年后的1000元相当于现在的228.11元，而100年之后的1000元只相当于现在的50元了。

因此，如果假设贷款利率也是$0.04$的话，那么今年借100万，30年后需要还324.34万，即大家常说的100万贷款和224.34万利息。但是根据上面通膨的折现算法，30年后的324.34万元就等于今天的100万，一分钱不多，一分钱不少。换句话说：

• 如果折现率小于房贷利率，那还款额折算到2020年大于100万，钱越借还得越多。
• 如果折现率大于房贷利率，那还款额折算到2020年小于100万，钱越借还得越少。

关键在于：钱本身没有价值，而是一个浮动的虚的参照。

既然钱只是一个参照，我们也可以用其他东西来参照，比如说，巨无霸。比如一个人在2008年借了100万，即8万的巨无霸。按照贷款利率$0.04$来算，2015年需要还钱131.16万，对应7.6万个巨无霸。也就说这里越借钱反而约富有。

再举一个例子，北京市1992年的平均年薪为3402。如果当年你借了10万元贷款，差不多相当于29.4年的收入。假设贷款分25年还清，利率为$0.045$。到期需要偿还约30万。而2017年北京市平均工资是101599，也就说偿还总金额仅相当于当年3年的年薪。

Reference

• 30年的房贷利息几乎等于本金，你是怎么看的？
• The Big Mac Index May Be Telling The Truth About Inflation
• Wiki - Time value of money
• 北京市历年社会平均工资（2019版）