Renormalization group analysis of stability of band crossing in spin-1 spin-orbit coupled degenerate Fermi gas

In one of my recent paper entitled Topological phases in spin-1 Fermi gases with two-dimensional spin-orbit coupling, we study the topological phases of Rashba spin-orbit (SO) coupled three-component Fermi gases. In fact, I also investigated the stability of the band crossings under repulsive $SU(3)$-invariant interactions, which is not included in the paper. In the following, I share my note on this matter.

Abstract

In this note, I unitize mean-field theory (MFT), Renormalization Group (RG) and scaling to study the (in)stability of band touching points including Dirac point and quadratic band touching (QBT) in spin-1 degenerate Fermi gases with Rsahba-like SOC.

Review of system Hamiltonian

The single-particle Hamiltonian in k-space is
$$ \begin{pmatrix} \delta_1-2t_s(\cos k_x + \cos k_y) & t_{so}(-\sin k_x + i\sin k_y) & 0 \\ -t_{so}(\sin k_x + i\sin k_y) & 2t_s(\cos k_x + \cos k_y) & t_{so}(-\sin k_x + i\sin k_y) \\ 0 & -t_{so}(\sin k_x + i\sin k_y) & \delta_2-2t_s(\cos k_x + \cos k_y) \end{pmatrix}. $$

If we only consider the touching points at $\Gamma$ point, the effective single-particle Hamiltonian becomes
$$\begin{pmatrix} \delta_1-(k_x^2+k_y^2) & t_{so}(-k_x + ik_y) & 0 \\ -t_{so}(k_x + ik_y) & k_x^2+k_y^2 & t_{so}(-k_x + ik_y) \\ 0 & -t_{so}(k_x + ik_y) & \delta_2-(k_x^2+k_y^2) \end{pmatrix},$$ where we also set $t_s=1$ (this does not affect the scaling since it can be treated as a mass term).

For QBT, we require $\delta_-=0$ and its low-energy Hamiltonian is
$$H_0 = \begin{pmatrix} 0 & (-k_x + ik_y)^2 \\ (k_x + ik_y)^2 & 0 \end{pmatrix}.$$

For the Dirac point, we only consider the cases when it appears between the lower two bands and consequently, $\delta_2=8$ is assumed (one may also set $\delta_1=1$ and investigate the problem, but those two cases are essentially the same). Now, we have
$$H_0 = \begin{pmatrix} 0 & -k_x + ik_y \\ -k_x - ik_y & 0 \end{pmatrix}$$ for the Dirac point.

Scaling and numeric renormalization

Before preceding, we first study the scaling of a massive (quadratic dispersion)
and massless (linear dispersion) Fermion fields respectively. A massive scaler (spinless) Fermi field can be described by the following Lagrange $\mathcal{L} = \phi^\dagger\frac{\partial\phi}{\partial\tau}+\frac{1}{2m}|\nabla\phi|^2 -\mu|\phi|^2-\frac{u}{2}\phi^\dagger\nabla\phi^\dagger\phi\nabla\phi$. At quantum critical point $\mu=0$ and $T=0$, such a a theory is invariant under scaling transformation $x’=xe^{-l}, \tau’=\tau e^{-zl}, \phi’=\phi e^{dl/2}$.

We choose dynamic critical exponent $z=2$ and the mass $m$ is assumed to remain invariant under scaling. Then we also have dim$[\mu]=2$ and dim$[u]=-d$. A similar argument for massless Dirac field $\mathcal{L} = \phi^\dagger_R\left(\frac{\partial}{\partial\tau} - iv_F\nabla\right)\phi_R+\phi^\dagger_L\left(\frac{\partial}{\partial\tau} + iv_F\nabla\right)\phi_L$ would give $x’=xe^{-l}, \tau’=\tau e^{-zl}, \phi_{R,L}’=\phi_{R,L} e^{l/2}$. We also require $z=1$ and dim$[\phi_{R,L}]=1/2$ holds for all dimension $d$.

Now, we consider an uniform $SU(3)$ invariant two-body contact interaction
$$V \sum_{i,\sigma\neq\sigma’} \hat{n}_{\sigma} \hat{n}_{\sigma’},$$
then we have dim$[V]=2-d$ and dim$[V]=d-1$ for a massive band touching and Dirac point respectively. Given our case $d=2$, $V$ is marginal (massive spinless fermion) or relevant (Dirac fermion).

Since the QBT is marginal, we calculate the RG beta function to one-loop order. Although it’s an effective two-level model, the third component is hardly mixed near the QBT. Giving the single particle Green function
$$G_0 = \begin{pmatrix} E-\sigma_k & \eta_k \\ \eta_k^* & E+\sigma_k \\ \end{pmatrix} ^{-1},$$
the one-loop correction counts two Feynman diagrams $(-1)\frac{i}{2\pi}\int dE\int\frac{d^2k}{(2\pi)^2}G_{0,ab}G_{0,ba}+(-1)^2\frac{i}{2\pi}\int dE\int\frac{d^2k}{(2\pi)^2}G_{0,aa}G_{0,bb} = \int\frac{d^2k}{(2\pi)^2}\frac{1}{2E_k}$, where $E_k=\sqrt{|\eta_k|^2+\sigma_k^2}$ is the single-particle energy.

Inserting back the effective Hamiltonian for QBT, we have $\beta(V)=\frac{dV}{dl}=\frac{1}{4\pi}V^2+O(V^3)$, where $l$ is momentum rescaling $k’=ke^{-l}$. Note that, this recovers exactly the QBT with $C_6$ symmetry and for $V>0$, the effective coupling would flow to strong coupling. One may also verify that the beta function vanishes at second order for Dirac points but $V$ is always relevant at second order for even higher band touching points with order $n>2$.

Mean-field theory

For the two-level model, we have the energy functional $E_{MFT}=\int dx\left(\psi^\dagger H_0\psi+Vn_an_b\right)$, where $\psi$ is the spinor wave function and we use $a,b$ to denote each charged Fermion field. The energy functional can be rewritten as $E_{MFT}=\int dx\left(\psi^\dagger H_0\psi - \frac{V}{4}(n_a-n_b)^2\right)$ to some constant with the particle number conservation assumption. Defining the order parameter $\delta=\langle \frac{V}{2}(n_a-n_b)\rangle$, and write the energy in terms of $\delta$, we have $E_{MFT}=\int dx\left(\psi^\dagger H_0\psi - 2\delta(n_a-n_b)+\frac{\delta^2}{V}\right)$.

Now, redefine the single-particle Hamiltonian $H_0=H_0-2\delta\sigma_z$, we can solve the following self-consistent equation $ \delta=\frac{V}{2}\int dE\int\frac{d^2k}{(2\pi)^2}(G_{0,aa}(k)-G_{0,bb}(k))$, to obtain the order parameter, where $G_0$ is single-particle Green function. This can be easily solved and we obtain $\delta=-\frac{2\pi}{V}+\frac{V}{8\pi}\Lambda^2$ and $\delta=\frac{\Lambda^2}{2}\text{csch}(\frac{4\pi}{V})$ ($\Lambda$ is energy cutoff) for Dirac point and QBT respectively.

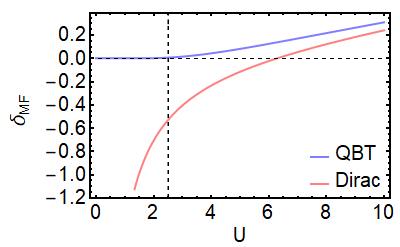
The result are plotted in the above figure and one can clearly observe that the Dirac point would achieve a finite mass term $-2\delta$ for arbitrarily weak interaction, thus it is instable when $V>0$. On the other hand, $\delta$ exponentially approaches $0$ when $V<\sqrt{2\pi}$ and is proportional to $V$ when $V\gg\sqrt{2\pi}$. This indicates that the QBT is stable against a finite interaction strength and can only be broken with sufficiently large interaction. We also remark that the instability (stability) of Dirac point (QBT) is independent of energy cutoff.

Self-energy correction

Now, we proceed to compute the self-energy correction using Hartree approximation $G^{-1}=G_0^{-1}+\Sigma_H$. The one-loop correction is given by
$$\begin{align}\Sigma_{H,ij}(k)&=(-1)\frac{i}{2\pi}\int dE\int\frac{d^2p}{(2\pi)^2}\big(G_{0,ia}(k)G_{0,bb}(p)G_{0,aj}(k)+G_{0,ia}(k)G_{0,ab}(p)G_{0,bj}(k)\\ &+G_{0,ib}(k)G_{0,ba}(p)G_{0,aj}(k)+G_{0,ib}(k)G_{0,aa}(p)G_{0,bj}(k)\big)\end{align},$$
where $i,j=a,b$.

Specifically, we have $$\Sigma_{H,aa}=\Sigma_{H,bb}=(-1)\frac{i}{2\pi}\int dE\int\frac{d^2p}{(2\pi)^2}\frac{E^3+E(\eta_k^*\eta_p+\eta_k\eta_p^*+\vert\eta_k\vert^2)}{(E^2-\vert\eta_p\vert^2)(E^2-\vert\eta_k\vert^2)^2}=0,$$ and

$$\begin{align} \Sigma_{H,ab}=\Sigma_{H,ba}^* &=\frac{i}{2\pi}\int dE\int\frac{d^2p}{(2\pi)^2}\frac{\eta_k^2\eta_p^*+E^2(2\eta_k+\eta_p)}{(E^2-\vert\eta_p\vert^2)(E^2-\vert\eta_k\vert^2)^2}\\ &=(-1)\int\frac{d^2p}{(2\pi)^2}\left(\frac{2\vert\eta_k\vert+\vert\eta_p\vert}{4\vert\eta_k\vert^3\vert\eta_p\vert(\vert\eta_k\vert+\vert\eta_p\vert)^2} \eta_k^2\eta_p^*-\frac{1}{4\vert\eta_k\vert(\vert\eta_k\vert+\vert\eta_p\vert)^2}(2\eta_k+\eta_p)\right)\\ &=\int\frac{d^2p}{(2\pi)^2}\frac{\eta_k}{2\vert\eta_k\vert(\vert\eta_k\vert+\vert\eta_p\vert)^2} \end{align}.$$

There are two distinct two-loop corrections and we first consider the one without momentum transfer, which is to count one-loop correction for the $G_0(p)$ terms
$$\begin{align} \Sigma_{H,aa} &=\Sigma_{H,bb}=(-1)\frac{i}{2\pi}\int dE\int\frac{d^2p}{(2\pi)}^2\int\frac{d^2q}{(2\pi)^2}\big(E^5+(E^3+E\vert\eta_k\vert^2)(\vert\eta_p\vert^2+\frac{1}{2}Re(\eta_q\eta_p^*))\\ &+E^3\vert\eta_k\vert^2+\frac{1}{2}Re(E^3(2\eta_p+\eta_q)\eta_k^*+E\eta_p^2\eta_q^*\eta_k^*)\big)/\left((E^2-\vert\eta_q\vert^2)(E^2-\vert\eta_p\vert^2)^2(E^2-\vert\eta_k\vert^2)^2\right) \end{align}$$
and it’s obviously trivial.

Acknowledgement

I thank Dr. T. Zeng from Westlake University for helpful discussions and conducting Exact Diagonalization (ED) numerics. The above results are consistent with ED.

Reference

• J. Hou, H. Hu, C. Zhang, Topological phases in spin-1 Fermi gases with two-dimensional spin-orbit coupling, arXiv 1809.04537.
• S. Sachdev, Quantum Phase Transition, Cambridge University Press, Cambridge, UK (1999).
• K. Sun, H. Yao, E. Fradkin, and S. A. Kivelson, Topological Insulators and Nematic Phases from Spontaneous Symmetry Breaking in 2D Fermi Systems with a Quadratic Band Crossing, Phys. Rev. Lett 103, 046811 (2009).